The most important data requirements are:

It can be helpful to standardize all variables except the target. Binarization is required for categorical data.

The basic procedure of the clustering model building is described in the chapter AdvancedMiner in practice (see the section Clustering model building ). Full specification of the model settings contains the elements of the Algorithm Settings: General Algorithm Settings , Learning Algorithm and Transformation Settings .

To create not only the clustering model but also the classification model it is necessary to use a combination of the classical SOM Kohonen algorithm and one of the algorithms from the LVQ family. The model is first trained using the SOM algorithm. Next it is trained using the chosen LVQ algorithm. This process is similar to incremental training, but in this case the algorithm is changed instead of the training data. It is also possible to use classical incremental learning techniques for SOM and LVQ learning by adding inputModel in MiningBuildTask .

LVQ algorithms were originally developed for Neural Gas networks. In AdvancedMiner they were adapted for Kohonen maps. The SOM algorithm gives very good results, so it is enough to use only several iterations of the LVQ algorithm.

Algorithm settings

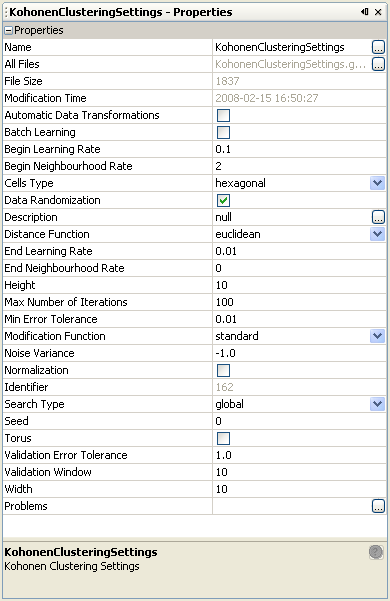
Table 36.1.  Kohonen Networks: Algorithm Settings for SOM and LVQ Algorithm

Name	Description	Possible values	Default value
Automatic Data Transformations	if TRUE automatic transformations (e.g. replaceMissing, binarization) should be executed, false otherwise.	TRUE / FALSE	FALSE
Batch Learning	enables/disables the batch learning process (faster but less accurate)	FALSE, TRUE	FALSE
Begin Learning Rate	the initial value of the learning rate	real numbers from the interval [0.0,1.0]	for LVQ: 0.1, for SOM: 0.3
Begin Neighborhood Rate	the initial size of the neighborhood	positive integer numbers	for LVQ: 0, for SOM: 2
Cell Type	the shape of the cells (neurons) in the Kohonen map	hexagonal	hexagonal
Data Randomization	decides whether to randomize the order of the training data in each iteration	FALSE, TRUE	TRUE
Distance Function	the function used to calculate the distance between neurons and training objects	euclidean, manhattan, minimum, maximum	euclidean
End Learning Rate	the final value of the learning rate, usually less or equal to beginLearningRate	real numbers from the interval [0.0,1.0]	for LVQ: 0.01, for SOM: 0.1
End Neighborhood Rate	the final size of the neighborhood, usually less or equal to beginNeighborhoodRate	positive integer numbers	0
Height	the vertical number of neurons in the Kohonen map	positive integer numbers	10
Number of Iterations	the maximum number of iterations of the learning process	positive integer numbers	for LVQ: 10, for SOM: 100
Min Error Tolerance	the acceptable error level; the learning process is stopped when the fitting error decreases below the specified error level	positive real numbers	0.01
Modification Function	the function used for the modification of the learning rate for neighborhoods	standard, uniform, Gaussian, linear, quadratic, reciprocal, quadraticReciprocal	standard
Noise Variance	the variance of noise provided into the data; when the value of this variance is equal to or less then zero noise is not provided into the data	non-negative real numbers	-1.0
Search Type	the winner searching algorithm	global, random, lastWin	global
Seed	the seed for random generator; when the value of this seed is equal to zero random generator is initialized with random value	real numbers	0
Torus	whether to equip the Kohonen map with a torus topology	FALSE, TRUE	FALSE
Validation Error Tolerance	the tolerance for error calculated on the validation data; learning process will be stopped when the value of current error calculated on validation data is greater than value of minimum ever calculated validation error multiplied by this tolerance	positive real numbers greater or equal to 1.0	1.0
Validation Window	the interval of fitting error calculated on the validation data. When this error increases the learning process will be stopped. When the value of this variance is equal to zero or validation data is not specified then this option is turned off.	positive integer numbers	10
Width	the horizontal number of neurons in the Kohonen map	positive integer numbers	10

Figure 36.4. Kohonen Networks: Algorithm Settings

Detailed descriptions of selected Algorithm Settings options:

• The Distance Function can be any of the following:

  • euclidean:

    

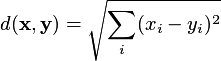
  • manhattan:

    

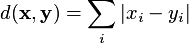
  • minimum:

    

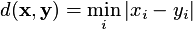
  • maximum:

    

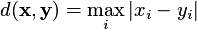
• The Modification Function can be any of the following:

  • standard:

    

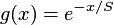
  • uniform:

    

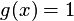
  • gaussian:

    

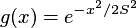
  • linear:

    

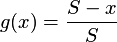
  • quadratic:

    

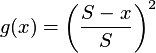
  • reciprocal:

    

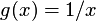
  • quadraticReciprocal:

    

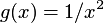
  where: 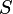is the largest acceptable neighborhood, and x is the size of the actual neighborhood.

• The following options are available for the Search Type

  • global: the winner is searched for among all the neurons in the Kohonen map,

  • random: the winner is searched for locally, starting from a randomly selected neuron,

  • lastWin: the winner is searched for locally, starting from the neuron that won in the previous iteration.

In addition to the settings specific to the Kohonen algorithm, the user can use Transformation Settings - to control the way of data transformation; these settings are described in the Transformation chapter.

Model statistics

The created model is represented by Self Organizing Maps. A tool called SOM Explorer can be used to create various visualizations of these maps.

Figure 36.5. The SOM Explorer

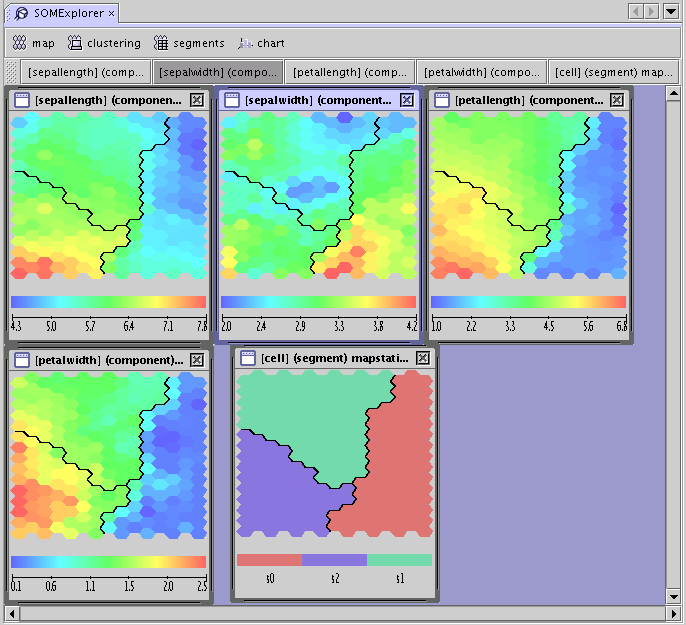
When it is required to visualize not only neuron weights (called components ) in a Kohonen map, but also some statistics for these neurons then it is necessary to run ComputeModelStatisticsTask first. The training data as well as new data with even more attributes can be used to compute the statistics. It is also possible to calculate statistics for data without some of the attributes used in the learning process. In this case an approximation of the calculated statistics is obtained.

All categorical variables (including the target variable) are automatically binarized, and the statistics are computed for binarized variables.