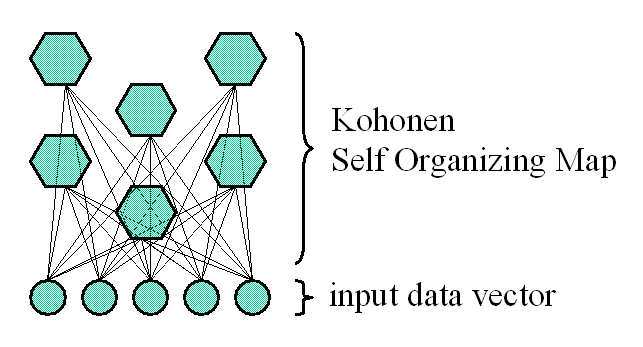
It can be assumed that the input data is represented by a
set of n-dimensional vectors
. The output is a two dimensional array of output nodes.
This array with output nodes becomes the data map in the
learning process. Every node (neuron) is represented by an
n-dimensional vector of weights.
These are the Self Organizing Maps. The dedicated learning algorithm was proposed by Teuvo Kohonen.
For each learning vector
:
the neuron nearest to the input learning vector is located. This neuron is called the winner (
):
The winner is assigned all the neurons
which are in a neighborhood relation with the
winner. The set of all these neurons is called the
neighborhood.
The winner's vector of weights is updated as follows:
where
is the learning rate.
Next the vectors of weights from the winner's neighborhood are updated according to the formula:
where
is a function which calculates the modification of
the learning rate for the neighborhood: a closer
neighborhood should learn more than a more distant
one.
Each learning vector is used once in each iteration. In the subsequent iterations the used neighborhood should be shrunk and the learning rate decreased.
AdvancedMiner implements three LVQ algorithms: LVQ, LVQ21 and LVQ3:
-
The LVQ algorithm is very similar to the classical SOM
learning algorithm. However, the rule for updating the
winner's weights is different:
if the winner (
) and the learning vector (
) are assigned to the same decision, then we
use the update formula as in the SOM
algorithm:
else:
-
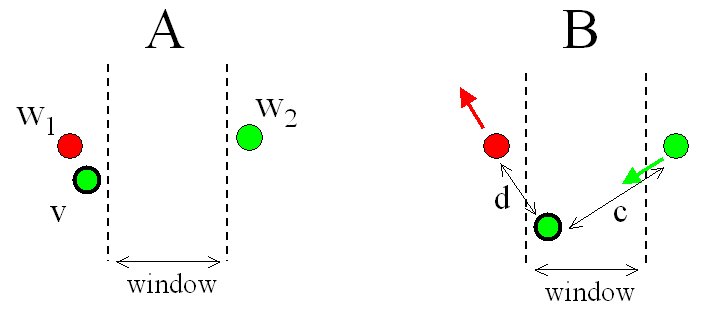
The LVQ21 algorithm uses the same updating rule of
winner weights as LVQ, but in this case there are two
winners (winner
and vice-winner
). The weights for both of them are updated only if the
following two conditions hold: (1) exactly one of them
has the same decision as the learning vector
and (2) the trained example falls into a special window
between the winners (situation B):
The LVQ3 algorithm differs from LVQ21 in only one way: the weights for both winners are updated only if at least one of them has the same decision as the learning vector.