Transition functions are used in Monte Carlo algorithms to calculate the next proposed point based on the previous one (i.e. the last one accepted in the chain). In AdvancedMiner it is possible to use transition functions based on distributions (independent sampling) and ones employing random walk methods.
A TransitionFunctionFromDistribution object is an adapter which allows any multivariate distribution to be treated as a transition function. This case is also known as independence sampling, because probability of drawing the next point does not depend on the previous one.
The syntax for the constructor is the following:
TransitionFunctionFromDistribution(distribution)
Tabela 9.10. TransitionFunctionFromDistribution methods
| Method name and syntax | Description of parameters | Output | Output type |
|---|---|---|---|
prob(x, y) | x - the source point (double[]) y - the destination point (double[]) | the probabilty of transition from point x to point y calculated as the probability of the adapted distribution in point y | double |
trans(x) | x - the source point | the next point drawn on the base of x | double[] |
setSeed(seed) | seed - the random number seed to use when drawing points | void |
The random walk algorithm of finding proposed points is commonly used in many real problems. It is based on sampling a new point around the old point with normal density.
The RandomWalkTransitionFunction constructor can be used in the following ways:
To create a transition function with the same variance in every dimension use the syntax:
RandomWalkTransitionFunction(dim, variance)To create a transition function for a distribution with a given variance vector use the syntax:
RandomWalkTransitionFunction(varianceVector)To create a transition function for a distribution with a given covariance matrix use the syntax:
RandomWalkTransitionFunction(covarianceMatrix)To create a transition function based explicitly on a distribution use the syntax:
RandomWalkTransitionFunction(distribution, tune, init[, forceSampling])In this case the covariance matrix is calculated using the formula
where
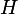is the Hessian of the sampling distribution calculated at its maximal point. This point
is found using the OptPPLibrary (the nonlinear optimization library).
Tabela 9.11. RandomWalkTransitionFunction constructor settings
| Parameter name | Parameter type | Description |
|---|---|---|
| dim | int | the dimesion of the problem |
| variance | double | the variance of a normal distribution (positive real values) |
| varianceVector | double[] | the variance vector of a multivariate normal distribution (positive real values) |
| covarianceMatrix | double[][] | the covariance of a multivariate normal distribution (positive real values) |
| distribution | a SamplingDistribution object | the sampling distribution |
| tune | double[] | a vector for modifying the covariance matrix |
| init | double[] | the initialization vector (strating point) for the optimization algorithm finding the maximal point of the sampling distribution |
| forceSampling | boolean | if set to true, in the case when the calculated Hessian matrix is not negative definite, it will be modified to become negative definite (false is default) |
Detailed description of selected RandomWalkTransitionFunction constructor parameters
- forcedSampling
- Occasionally it is not possible to find the maximum of a distribution using numerical methods and the calculated Hessian in the approximate maxmum in not negative definite. In such situations if this parameter is set to false, the exception wil be thrown and if is set to true, small values will be added to the main diagonal of the Hessioan until it becomes negative definite.
In addition to the three TransitionFunctionFromDistribution methods the RandomWalkTransitionFunction objects also have the methods described in the table below.
Tabela 9.12. RandomWalkDistributionFunction methods
| Method name and syntax | Description of parameters | Output | Output type |
|---|---|---|---|
optimizeCovariance(sampler, optimal, testLength, maxSteps, eps) | sampler - a MetropolisSampler object with this random walk transition function set as its transition function optimal - the required acceptance ratio (double) testLength - the length of the chain on which to test the acceptance ratio (int) maxSteps - the maximal number of steps for best tune search (int) eps - the accepted difference from the required acceptance ratio (double) | the best tune by which to multiply the current covariance matrix to obtain the required acceptance ratio | double |
dist() | the multivariate normal distribution associated with this transition function | MultivariateDistribution | |
setDist(distribution) | distribution - the distribution to associate with this transition function | void | |
getMsg() | a message generated while searching for the optimal covariance matrix (if any) | String |
Detailed description of selected RandomWalkTransitionFunction methods
- optimizeCovariance
- This method is used to obtain a covariance matrix with an approximate optimal acceptance ratio. The algorithm starts from the current matrix and multiplies it by some factor. If the acceptance ratio on a generated sample of lenght equal to testLength is less than required the factor will be decreased, otherwise the factor will be increased and the next sample will be generated and examined. The algorithm stops when the acceptance ratio for the found factor approximates the optimal acceptance ratio with error lesser than eps or after performing maxSteps steps.